倍数に関する問題

例題 1	1 から 10 までの数字が 1 つずつ書かれたカードが 1 枚ずつ合計 10 枚ある。 このカードから同時に 3 枚を選ぶとき，選ばれた 3 枚の数の和が 3 の倍数となる確率を求めよ。

全事象は，₁₀C₃ = 120 通りあり，それらは同様に確からしい。
また，カードをあらかじめ次のようにグループ分けしておく。
A : 3 の倍数・・・ 3，6，9
B : 3 で割った余りが 1　・・・ 1，4，7，10
C : 3 で割った余りが 2　・・・ 2，5，8

[a]　3 枚とも A グループから選ぶとき，1 通り
[b]　3 枚とも B グループから選ぶとき，4 通り
[c]　3 枚とも B グループから選ぶとき，1 通り
[d]　A，B，C から1 枚ずつ選ぶとき，3 × 4 × 3 = 36 (通り)
以上の事象 [a]〜[d] は互いに排反であるから，求める確率は，

1 + 4 + 1 + 36	=	21
120		60

全体の枚数が 3 の倍数のときは必ず 1/3 となりそうです。

例題 2	1 から 10 までの数字が 1 つずつ書かれたカードが 1 枚ずつ合計 10 枚ある。 このカードから同時に 3 枚を選び，選ばれた 3 枚の数の積を X とする。 (1)　X が奇数である確率を求めよ。 (2)　X が偶数である確率を求めよ。 (3)　X が偶数であるが，3 の倍数でない確率を求めよ。 (4)　X が 6 の倍数である確率を求めよ。

全事象は，₁₀C₃ = 120 通りあり，それらは同様に確からしい。

(1)	3 枚とも奇数のカードを選ぶ事象であるから，求める確率は， 5C3 = 1 120 12
(2)	余事象は 3 枚とも奇数のカードを選ぶ事象であるから，求める確率は， 1 ー 1 = 11 12 12
(3)	まず，選んではいけないのは，3, 6, 9 の 3 枚です。 残った 7 枚のうち，偶数は 2, 4, 8 の 3 枚，残りの 4 枚は奇数です。 3 の倍数でない 7 枚のカードから 3 枚を選ぶ方法は，7C3 通り このうち，3 枚とも奇数のカードである選び方は，4C3 通り 以上より，求める確率は， 7C3 ー 5C3 = 25 = 5 120 120 24
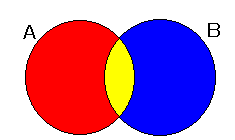
(4)	積が 6 の倍数となる事象を直接考えるのは大変です。 余事象は，積が「偶数でない」または「3 の倍数でない」となります。 （下のベン図の、「色のない部分」が、6 の倍数となる部分です。) [A]　X が偶数でないとき すべて奇数の札を取り出すから、5C3 = 10 (通り) [B] X が 3 の倍数でないとき 3 の倍数でない札は 7 枚あるから，7C3 = 35 (通り) [C] X が偶数でも 3 の倍数でもないとき 該当する札は，1，5，7 の 3 枚しかないので，取り出し方は 1 通り 以上より，求める確率は， 120 ー (10 + 35 ー 1） = 76 = 19 120 120 30

例題 3	n 個のさいころを 1 回振って，出た目の積を X とする。 (1)　X が 4 の倍数となる確率を求めよ。 (2)　X が 6 の倍数となる確率を求めよ。

反復試行ですが，考え方は例題 2 と同じです（繁雑な計算を避けるため，あえて n 個にしてあります）。

(1)	まず，X が偶数となる事象の余事象は「すべて奇数の目がでる」事象ですから，X が偶数となる確率は， 1 ー 1 2n X が偶数となる事象のうち，除かれるものは「X が 4 の倍数とならない」事象であり。 これは「1 個だけ (2 または 6)の目が出て，残りは奇数の目が出る」事象である。 nC1 × 21 × 3n ー 1 = 2n = 2n 6n 6 × 2n ー 1 3 × 2n よって，求める確率は， 1 ー 1 − 2n = 1 ー 2n + 3 2n 3 × 2n 3 × 2n
(2)	全事象は 6n 通りあり，それらは同様に確からしい。 また，X が奇数となる事象を A，X が 3 の倍数でない事象を B とする。 事象 A は，n 個とも奇数がでる事象であるから，3n 通り 事象 B は，n 個とも「1，2，4, 5」が出る事象であるから，4n 通り また，事象 A ∩ B は，n 個とも「1，5」が出る事象であるから，2n 通り 事象 A ∪ B が求めたい確率であるから， 1 ー 3n + 4n − 2n = 6n ー 3n ー 4n + 2n 6n 6n