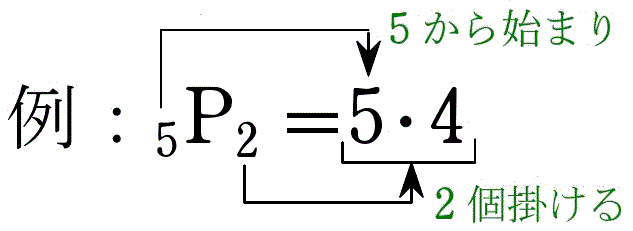定義
n 個の異なるものから,1 つずつ合計 r 個取り出して,1 列に並べたものを,
n 個から r 個取り出した順列 といい,記号で nPr と表す。
特に,n = r のときは nPn = n! と表し,これを n の階乗という。
また,0! = 1 と定める。
|
3 つの下線の条件がすべて揃ったときに限り,記号 P を用います。
P は Premutation の頭文字です。n! のほうは全員を並べると理解して良いです。
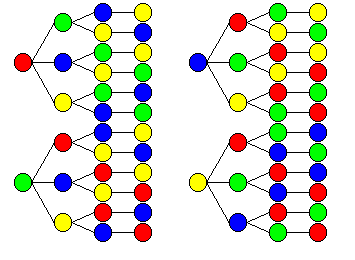
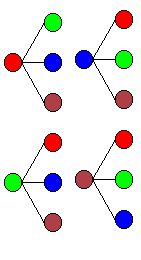
下の樹形図の左が 4! となる例,右が 4P2 となる例です。
| 4!(異なる 4 つの球を全て使って並べる)
| 4P2(4 つの異なる球から 2 個を選んで並べる)
|
|---|
| 
|
|---|
計算ルール
上の例のとおり,樹形図の「枝」が 1 つずつ減っていくのが特徴です。
このことから,次の式を得ます(掛け算の記号がうるさいので・で表示します)。
n! = n(n - 1)(n - 2)・…・2・1 (1 になるまで掛け続ける)
記号 P の計算方法は次の図のとおりです。
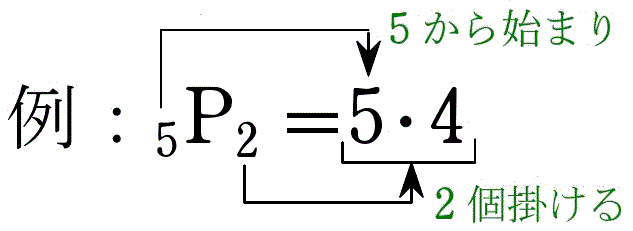
例えばこの 5P2 に,3・2・1 を掛けると 5! となります。
一般に,n 個から r 個を取り除くと n - r 個残るので,
nPr ×(n - r)! = n!
が成り立ち,両辺を (n - r)! で割ると,
約分すると,nPr = n(n - 1)(n - 2)・・・(n - r + 1) となります。
(式の重要度は [1] のほうが高いです。)
ここで,[1]の両辺に n = r を代入すると,
|
nPn = | n! | = | n! | となってしまいます。
| | (n - n)! | 0!
|
定義より, nPn = n! ですから,0! = 1 と定める必要が出ます。
例: 7 人から 3 人を選び,1 列に並べる方法は,7P3 = 7・6・5 = 210 (通り)
紹介しておいて変な話ですが,「場合の数・確率」に限れば記号 P を使わないと解けない問題は少ないと思います。
(もちろん,使ったほうが早い問題はいくらでもあります。念のため…)
記号 P を使う場面が少ないからと言って不安になる必要はないでしょう。
nPr の計算機です。n ≧ r となるよう,半角の数値を入力してください。
P=
|