どの 3 点も同一直線上にない，n 個の点を頂点とする三角形は，全部で nC3 個あります。
ここでは，これにいろいろな条件をつけた問題を考えます。
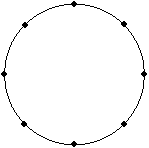
| 例題 1 | 円を 8 等分した点を頂点とする三角形を考える。
(1) 全部で何個の三角形が作れるか。
(2) 直角三角形は何個作れるか。
(3) 二等辺三角形は何個作れるか。
| 
|
|---|
| (1) | 8 個の点はどの 3 点も同一直線上にないので，8C3 = 56 (個)
| | (2) | 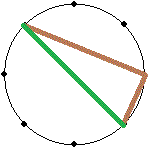 円に内接する直角三角形の 1 辺は直径です。これを用いると，
まず直径を選び，残った点から 1 点を選ぶと直角三角形が 1 つ定まります。
よって，4 × 6 = 24 (個)
一般に，n が偶数のときは直角三角形を作ることができます。
| 直径の個数は | n | 個あり，n − 2 個の点が残るので，
| | 2
|
| n が偶数のとき, 直径直角三角形は | n(n − 2) | 個できます。
| | 2
|
| | (3)
| 
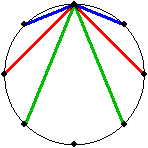1 点を定めると，その点を一方とする直径を対象な 2 点を選べば，二等辺三角形が 1 つ定まります。
n = 8 のときは，右の図のように，1 点を定めると 3 つの二等辺三角形を作ることができます。
よって，8 × 3 = 24 （個）
一般には，正三角形が発生することがあるため，紹介は控えます…
|
| 例題 2
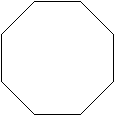
| 正八角形の頂点を結んでできる図形を考える。
(1) 正八角形の対角線は何本あるか。
(2) 正八角形の頂点を結んでできる三角形のうち，
正八角形と辺を共有しないものは何個あるか。
| 
|
|---|
| (1)
| 8 個ある頂点から 2 点を選ぶと直線が 1 つ定まりますが，うち 8 本は「辺」です。
よって，8C2 − 8 = 48 (本)
|
一般にも，凸 n 角形の対角線の本数は，nC2 − n =
| n(n − 3) | (本)です。
| | 2
|
| (2) | 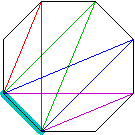 全部で 56 個ある三角形のうちから，次のものを除きます。
[A] 三角形が正八角形が 2 辺を共有するもの
頂点を定めると自動的に決まるから，8 個
[B] 三角形と正三角形がちょうど 1 辺を共有するもの
共有する辺の選び方は 8 通り
選ばれた辺に対して，共有する辺が 1 点となれる頂点は 4 個ある。
よって，ちょうど 1 辺を共有するものは，8 × 4 = 32 （個）
以上より，正八角形と辺を共有しない三角形は，56 − 8 − 32 = 16 （個）
| |
| 例題 3
| n ≧ 6 の凸 n 角形を F とする。
F の頂点を結んでできる三角形のうち， F と辺を共有しないものは何個あるか。
|
|---|
F と 2 辺を共有する三角形は n 個，
F と 1 辺のみを共有する三角形は n( n − 4) 個
よって，F の頂点を結んでできる三角形のうち， F と辺を共有しないものは，
nC3 − n − n( n − 4)
| = | n( n − 1)( n − 2) | =(略)= | n( n − 4)( n − 5)
| | 6 | 6
|
n = 4，5 のとき，辺を共有しない三角形は作れないので（0 個だから），この式は n ≧ 4 でも成り立ちます。
|