円順列と数珠順列について

「(机の上に)円形に並べる」とは，「回転させて重なるものは同じとみなす」ということです。
下の 5 つは，回転させると重なるので，同じものです。

格言 5　図形は固定して考えよ。

例題 1 のように，円形以外に条件のないときは，どれを固定してもかまいません。
たとえば緑を固定すると，残りの 4 か所は自由になります。
よって，4! = 24　(通り)
一般に，n 個のものをすべて使ってできる円順列は， (n−1)! 通りあります。

例題 2　緑、赤、青、黄、茶色の５つの球を円形に並べるとき、 緑と赤の球が隣り合うような並べ方は何通りあるか。

緑と赤は対等なので，どちらを固定してもかまいません。
赤を固定すると，緑はその隣の 2 通りの入れ方がある。
残りの 3 か所は自由に入れてよいので，3! 通り
以上より，2×3! = 12　(通り)
下に，この様子のスライドを入れておきます。

まず，赤を固定

例題 3　Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ の６人を円形に並べるとき，ＡとＢが向かい合う並べ方は何通りあるか。

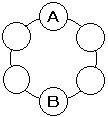
Ａさんを固定すると，Ｂさんは自動的にその反対側となります。(1 通り)
残りの 4 人は自由だから，4! = 24　(通り)

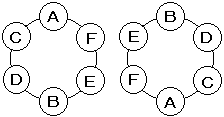
…それでもＡさんとＢさんをひっくり返したくなる人へ…
下の 2 つは同じですよね？

例題 4　男子 3 人、女子 3 人を円形に並べるとき，男女交互になるような並べ方は何通りあるか。

例えば女子の A さんを固定します。
残りの女子は，2 か所に入るので，2! 通り
残った男子は 3 か所に入るので，3! 通り
以上より，2!×3! = 12　(通り)
これも，下にスライドを用意しておきますので，ゆっくり理解しましょう。

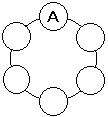
まず，赤を固定

例題 5　7 人から 4 人を選んで円形に並べる方法は何通りあるか。

P か C かで迷ったら，C を選び，作業を分けましょう。
7 人から 4 人を選ぶ方法は，₇C₄ 通り
選ばれた 4 人が円形に並ぶ方法は，(4−1)! = 3!　(通り)
以上より，₇C₄ × 3! = 35 × 6 = 210　(通り)

例題 6　5 つの異なる球に、穴をあけてネックレスを作る。異なるネックレスは何個あるか。

ネックレス（数珠、腕輪など）を作るときは，回転させて重なるだけでなく、
下のように「ひっくり返して重なる」ものも同じとみなします。

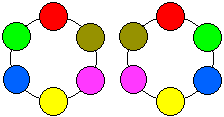
よって，5! ÷ 2 = 60　(個)