|
例題 2 | 赤玉が 1 個,青玉が 2 個,緑玉が 3 個ある。
この 6 個の玉すべてに穴を空け,ひもを通してネックレスを作る。
異なるネックレスは何個できるか。
|
|---|
単純に 2 で割って良いときは,「すべてが左右非対称」のときだけです。
例題 1 で数えた 10 個のうち,左右対称のものが 2 個あります(下の図)
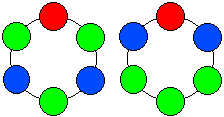
左右対称のものは,裏返しても自分自身なので,2 で割ることができません。
残った 8 個は,左右非対称なので,裏返すと重なります。
以上より,異なるネックレスは,4 + 2 = 6 (個)
|
例題 3 赤玉 2 個,青玉 2 個,緑玉 2 個すべてを使って円形に並べる方法は何通りあるか。
|
すべて 2 個ずつあるので,試しに赤の 1 つを固定します。
残りの 5 個の並べ方は,
もちろん,回転して重なるものは同じとみなします。(下はその 1 例)
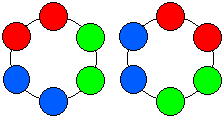
2 で割りたいですが,回転しても自分自身になるものが下の図のように 2 つあります。
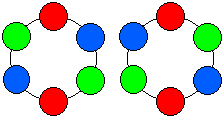
残りの 28 個は回転させると同じになるので,2 で割ります。
よって,全部で 14 + 2 = 16 (通り)
|