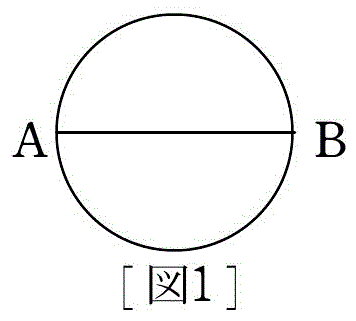
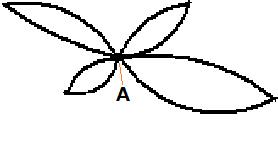
例題 3 次の図のような道を一筆書きで結ぶ方法は何通りあるか。
|
一筆書きは例外を除けば，交差点が始点となります。
（図１の直径 AB がなくなってしまうと円ですから，始点が無数に存在します。）
図１に話を戻すと，始点は A, B のどちらでもよさそうです。
まず，A を始点として考えてみます。
A を出発するとき，その道の選び方は 3 通り。
B から A に引き返すときは (道を 1 本使ってしまったから) 2 通り
A に戻って再び B に戻る方法は 1 通り
以上より，A を始点とした場合は 3×2×1 = 6 (通り)
ここまでは，3! 通りと考えてよいでしょう。
しかし，B を始点とした場合も同じだけあるので，
求める場合の数は 2×6 = 12 (通り)
一般に，異なる 2 点 A, B を結ぶ道がちょうど n 本あり，A, B のいずれかを始点とする一筆書きの方法は，
n!×2 通りあります。
念のため…
n = 1 のときは線分 AB 間の一筆書きなので 2 通り。
n = 2 （一般に偶数）のときも，「A または B を始点とする」と限れば，成り立ちます。
n が奇数のときは始点と終点は異なり，偶数のときは(始点が指定されていれば)始点に戻ってきます。
（出題者目線の蛇足）AB 間を結ぶ道が奇数本のときは始点を定める必要はありませんが，
偶数本ある（さらに拡張して，始点と終点が一致する）場合は始点(の候補)を指定しないと，
解答は「無数に存在する」となってしまいます。
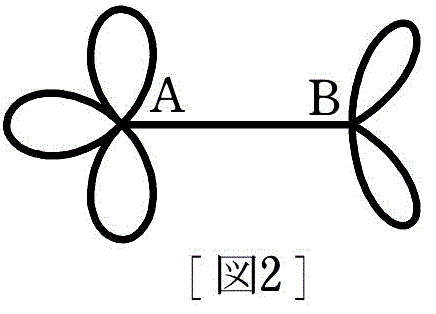例題 4 次の図のような道を一筆書きで結ぶ方法は何通りあるか。
|
AB を結ぶ道が 1 本しかないので，A の中で一筆書きが完結するものと，B の中で完結するものに分けます。
A の中で完結する一筆書きについて
最初は 6 通り選べますが，どれを選んでもそのまま A に戻ってしまいます。
つまり，2 回目の道の選択肢は 4 通りに減り，3 回目は 2 通りとなります。
以上より，A の中で完結する一筆書きは，6×4×2 = 48 (通り)
B の中で完結する一筆書きも同様に，4×2 = 8 (通り)
さらに，始点の選び方が（A，B の）2 通りあるので，求める場合の数は，
48×8×2 = 768 (通り)
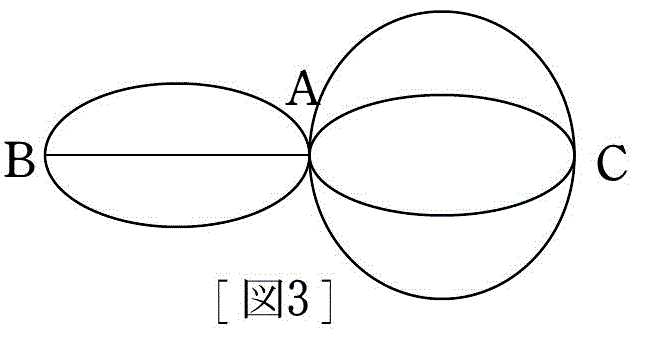例題 3 次の図 3 のような道を一筆書きで結ぶ方法は何通りあるか。
|
まずは始点の候補を割り出しましょう。
もし C を始点にすると，B に行くことを考えなくても C に戻ってしまいます。
A が始点のとき，どの方法も B を 1 回，C を 2 回経由して B に至ります。
この並べ方は 3 通りです。（→同じ文字を含む順列）
また，道の選び方は AC 間で 4! = 24 (通り)，
AB 間の道の選び方は 3! = 6 (通り)
B を出発するときも同じだけあるので，求める場合の数は，
3×24×6×2 = 864 (通り)
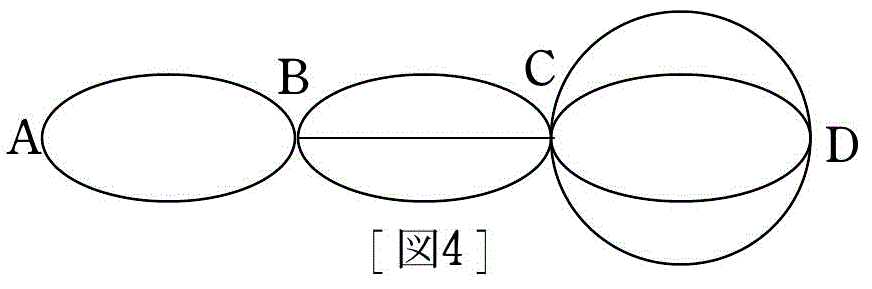例題 5 次の図 4 のような道を一筆書きで結ぶ方法は何通りあるか。
|
AB 間の道が 2 本，BC 間が 3 本，CD 間が 4 本あるので，始点は B または C です。
A を無視して考えると，例題 3 と同じ問題になることに着目します。
＜解答＞
A を無視して考えると，B から C へ向かう経過点の並べ方は 3 通りある。
例えば BCBCDCDC と結んだとき，「B」を「BAB」に取り換えると，図 4 の一筆書きの 1 つができる。
その取り換える方法は 2 通り。
道の選び方について，AB 間は 2! 通り，BC 間は 3! 通り，CD 間は 4! 通りある。
さらに，始点の選び方が 2 通りあるから，求める場合の数は，
2×3×2!×3!×4! = 3456 (通り)
出てきた数値にニヤリとしてしまいました。(笑)
| 
