|
例題 1 赤玉 3 個,緑玉 2 個,青玉 3 個を 1 列に並べる方法は何通りあるか。
|
 考え方 1
考え方 1
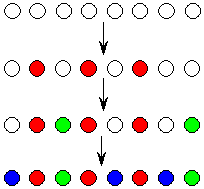
まず,右図のように,8 個の白玉を並べておきます。
このうち,3 個を赤玉に取り換える方法は,8C3 通り
残った(5 個の)白球のうち,2 個を緑玉に取り換える方法は,5C2 通り
最後の青玉を取り換える場所は,自動的に定まる。
以上より,8C3 × 5C2 = 560 (通り)
考え方 2
8 個の玉すべてに区別がついたとすると,その並べ方は 8! 通り
ここで,赤,緑,青の各色について,それぞれ 3!,2!,3! 通りずつに区別がつかなくなるから,
| 8! | = | 8・7・6・5・4・3・2・1 | = | 8・7・6・5・4 | = 560 (通り)
| | 3!2!3! | 3・2・1・2・1・3・2・1 | 3・2・1・2・1
|
| 8C3 × 5C2 =
| 8・7・6・5・4 | となり,どちらの考え方も正しいことが分かります。
| | 3・2・1・2・1
|
| 例題 2
| (1) KYOTO の 5 文字を並び替えた文字列は何個あるか。
(2) KAWASAKI の 8 文字を並び替えた文字列は何個あるか。
|
このようなテーマがなくても,飛びついてしまう前に冷静に文字を見渡しましょう。
どちらにも,同じ文字が含まれているので,考え方 2 で解くことにします。
| (1) 5 文字あるうち,O が 2 つ含まれるから, | 5! | = 60 (個)
| | 2!
|
| (2) 8 文字あるうち,K が 2 つ,A が 3 つ含まれるから,
| 8! | = 3360 (個)
| | 2!3!
|
|
例題 3 0,0,1,2,2,3,3 の数字すべてを使ってできる 7 桁の整数は何個あるか。
|
0 入り順列の応用です。1 だけ,1 個しかありません。
条件があるのは最高位だけなので,最高位に使われる数によって場合分けします。
| [A] | 最高位が 1 のとき
| 残った 6 桁で使える数はそれぞれ 2 個ずつあるから,
| 6! | = 90 (個)
| | 2!2!2!
|
| | [B] | 最高位が 2 または 3 のとき
最高位の選び方は 2 通りあり,どちらの場合も 0 が 2 個
最高位で使わなかった数が 2 個残る。
|
以上[A],[B] より,90 + 360 = 450 (個)
例題 4 [2010年 弘前大学] G,O,U,K,A,K,U の 7 文字を 1 列に並べるとき,
同じ文字が隣り合わないような並べ方は何通りあるか。
|
「隣り合わない」は条件のないものを先に並べる,というお約束に従います。
条件のない G,O,A の並べ方は 3! 通り
例えば △G△O△A△ として,この△のうちの 2 つを U に取り換える方法は,4C2 通り
さらに,例えば □U□G□O□U□A□ として,この□のうちの 2 つを K に取り換える方法は,6C2 通り
以上より,このときの並べ方は,3! × 4C2 × 6C2 = 540 (通り)
ただし,以上の方法では U の間に G,O,A が少なくとも 1 つ入るため,「UKU」と続くものは含まれていない。
ここで,G,0,A,K,[UKU] の並べ方は,5! = 120 通りある。
以上より,全部で 540 + 120 = 660 (個)
難問であればあるほど,今までの経験値を生かすことが重要になってきます。
良い研究者は地道に努力と経験を重ねて新しいことを発見(発明)します。
そういう学生が欲しいのだというメッセージを感じた問題でした。
|