条件付き確率について

例えば，「１０代の人のうち，学生は X ％」とか，
「学生である人のうち，１０歳台である Y ％」」といったように，
対象を絞って統計をとることがよくあります。
普段は意識しないだけで、これらが条件つき確率と呼ばれるものの１つです。
目に見えるデータなら兎も角，目に見えなくなった途端に難しく感じる生徒が多いように感じます。

定義

ある試行について，事象 A が起こった条件下で，事象 B が起こる確率を，
A の下で B が起こる条件付き確率いい，記号で PA(B) と書く。
また，A の下で B が起こる条件付き確率を以下の式で定義する。
PA(B) ＝P(A ∩ B)＝n(A ∩ B)
P(A)n(A)

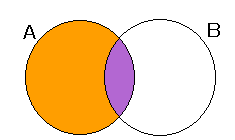
なぜ分子がP(A ∩ B) なのか，不思議に思うかもしれません。
事象 A が起こっているのが前提になるので，
事象 B のうち，A でない部分があっても関係ないからです（右図）。
条件つき確率の計算はほとんど，右の「個数分の個数」で解くことが出来ます。
(中央の「確率分の確率」を使うときは困ったとき用です。)
例題 1-1 　右の図はある献血センターでとった統計である。
(1)　血液型が A である人のうち，年齢が 10 代である割合を求めよ。
(2)　年齢が 10 代である人のうち，血液型が A である割合を求めよ。
年齢＼血液型Aそれ以外
10代50150
それ以上350650
(1)　は対象が A 型に絞られているので， 50/400 = 1/8 です。
(2)　は対象が 10 代に絞られているので，50/200 = 1/4 です。
分子はいずれも共通部分 (50人) を見ていますから，分子が A ∩ B となるのです。
また，例題 1-1 の問題は次のようにも置き換えられます。
例題 1-2 　例題 1-1 で訪れた 1200 人のうちから無作為に 1 人を選ぶ
(1)　血液型が A であるとき，年齢が 10 代である確率を求めよ。
(2)　年齢が 10 代であるとき，血液型が A である確率を求めよ。
「であるとき」という表現でつまずいてしまう場合は，上の 1-1 のことだと置き換えて考えましょう。

例題 2 　3 本の当たりくじを含む 10 本のくじがあり，A さんと B さんがこの順でくじをひく。
A さんが引いたくじはもとに戻さないとき，次の確率を求めよ。
(1)　A さんが当たりくじを引いたと判ったとき，B さんが当たりくじを引く確率を求めよ。
(1)　A さんがはずれくじを引いたと判ったとき，B さんが当たりくじを引く確率を求めよ。

B さんが引くとき，全体は必ず 9 本に減っています。当たりくじが減るかどうかなので，
(1) は2であり，(2) は3です。
99
このように 2 つの試行が互いに影響し合うとき，これらは従属である，といいます。
本来くじ引きは平等なのですが， 後で引く B さんが不公平に感じるのは，条件付き確率による錯覚です。
この条件付確率で感情が左右されてしまわいよう，プロ野球のドラフト抽選では，あらかじめ封をして，
結果がすぐに分からないようにしてあるのです。

確率の乗法公式 (独立と従属の違い)

定義の式の両辺に P(A) を掛けると，次の等式が成り立ちます。
P(A ∩ B) = P(A) × PA(B)

例題 3 　3 本の当たりくじを含む 10 本のくじがあり，A さんと B さんがこの順でくじをひく。
A さんが引いたくじはもとに戻さないとき，次の確率を求めよ。
(1)　2 人とも当たりくじを引く確率
(2)　B さんが当たりくじを引く確率

(1)
　1 本目が当たりである確率は3，
10
1 本目が当たりである条件下で，2 本目も当たりである確率は，例題 2 より，2
9
以上より，求める確率は，3×2=1
10915
(2)
　Aさんがはずれを引いたのち，B さんが当たりくじを引く確率は， 7×3＝7
10930
これと (1) より，求める確率は， 2+7＝3
3010
これより，A さんも B さんも，当たりくじを引く確率は 3/10 となり，実は平等であることが判ります。
ここでは (1)が P(A ∩ B) であり，(2) が P(B) なので，
試行が独立のときの等式 P(A ∩ B) = P(A) × P(B) は成り立ちません！
同じ掛け算だから混同してしまうかもしれません。(私もかつてはそうでした。不明を恥じています・・・)
３人以上でも，くじ引きが平等であることの理由は分けて説明します。

例題 4 　3 本の当たりくじを含む 10 本のくじを 1 本ずつ封筒に入れてよくかき混ぜる。
この中から 同時に 2 枚の封筒を選び，選ばれた封筒の 1 枚を開いたら当たりであった。
このとき，もう 1 枚の封筒の中身も当たりくじである確率を求めよ。

現実にあり得るような設定で文章を書くと，上のように非常に長くなるため，
次のような不自然な書かれ方になることがあります。

（例題 4 の言い換え）
3 本の当たりくじを含む 10 本のくじから同時に 2 本を引いた。
一方が当たりであるとき，他方も当たりくじである確率を求めよ。

不自然な場所に「とき」があるときは，条件付き確率です。
例題 4 の言い換えでも，「一方が当たりであるとき」となっています。
この時点では，他方が当たりかどうかはわかりません。
（逆に，「少なくとも一方が当たりである」と読んでください。）

つまり，「分母」は，「当たりが 1 本以上含まれる」事象を考える必要があります。
分子は，このうち，「2 本とも当たりである」事象です。まとめると，次のようになります。

[A]　1 本が当たりで，もう 1 本がはずれのとき
このような選び方は，3 × 7 = 21 （通り）
[B]　2 本とも当たりであるとき
このような選び方は，10C2 = 45 （通り）
以上より，求める確率は，45 = 15
21 + 4522

例題 5 　3 つのさいころを同時に投げる。
出た目の少なくとも 1 つが 5 であるとき，3 つの目の積が奇数である確率を求めよ。

余事象が多い問題は確率を用いたほうが分かりやすいかもしれませんね。

下線部について，単に「すべて奇数」だと (1,1,1) など，91 通りの中に含まれていないものも数えてしまいます。
あくまで分子は A∩B の場合の数であることに注意しましょう。

練習問題へ
関連：原因の確率
Back