じゃんけんをして１人が勝ち残るには？

ここでは、ジャンケンをして１人が勝ち残る確率と、そうなるまでの回数の期待値を考察したいと思います。
２人になっても、何を出すかはかならず１／３であるとします。 ジャンケンの基本については、こちらをご覧下さい。

まずは２人からいきましょう。
１回でＡの勝つ確率は１／３、Ｂの勝つ確率は１／３、「あいこ」の確率は１／３です。
１回で勝敗のつく確率は２／３ということになります。
ｎ回目で決まる確率は、ｎ−１回「あいこ」が続いた後に勝敗がつくわけですから、
１／３n-1＊（２／３）＝２／３nです。
よって、勝敗がつくまでじゃんけんを続ける回数の期待値は、
無限級数の和の公式より、
（２／３）＊Σ(n=1 to ∞)（ｎ／３n-1）＝（２／３）＊｛１÷（１−1/3）｝2＝３／２＝１．５
確かに、２人でじゃんけんすれば、１，２回で勝負がつきます。

一般に、ｎ人でじゃんけんをして初めて勝負がつくまでの回数の期待値は、
３n-1／（２n−２）回です。

３人でじゃんけんをした場合 １回の勝負で１人が勝つ確率は１／３
１回の勝負で１人が負ける確率は１／３
３人とも残ってしまう確率は１／３

２回で１人が勝ち残る確率は、つぎの２つが考えられます。
（１）１回目は１人だけ負け、２回目は２人で勝負をする　(1/3)＊(2/3)＝２／９
（２）１回目では勝敗がつかず、２回目で１人が勝つ　(1/3)＊(1/3)＝１／９

よって、２回目で１人が勝ち残る確率は３／９です。
３回目も１／３である筈は無いですね。もう少し様子を見て見ましょう。
３回目で１人が勝ち残る確率（例えば３→２→１のときは、あいこ、１人負け、１人勝ちの順です）
（１）３→３→１　のとき　(1/3)＊(1/3)＊(1/3)＝１／２７
（２）３→２→１　のとき　(1/3)＊(1/3)＊(2/3)＝２／２７
（３）２→２→１　のとき　(1/3)＊(1/3)＊(2/3)＝２／２７
よって、３回目で１人が勝ち残る確率は５／２７です。

４回目で１人が勝ち残る確率
（１）３→３→３→１　のとき　(1/3)3*(1/3)＝1/81
（２）３→３→２→１　のとき　(1/3)*(1/3)*(1/3)*(2/3)＝2/81
（３）３→２→２→１　のとき　同様に2/81
（４）２→２→２→１　のとき　同様に2/81
よって、４回目で１人が勝ち残る確率は７／８１です。

以上のことからｎ回目で１人が勝ち残る確率を予測すると、
(２ｎ−１)/３nとなります（証明略）。
よって、求める期待値は、公式より、

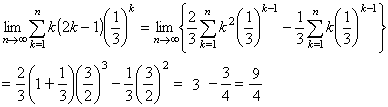
およそ２．５回ということになります。（らすかるさんのお蔭で訂正できました）
３人に増えるだけで、こんなに複雑になるのですね。

さて、より良い解法をらすかるさんから頂きました。

条件付き期待値を利用する考え方

上の３人でじゃんけんをした場合について、条件付き期待値という考え方を使ってみます。
まず、３人でじゃんけんしたときに勝負がつくまでにかかる回数の期待値は、
３2／（２3−２）＝３／２回…Ａです。
仮にここで一人だけが勝ち残った場合、この３／２回で確定です。
次に、２人が残った場合を考えると、
２人が勝ち残る確率は3Ｃ2／３2＝１／３です。
この１／３が起こった条件の下で、勝負が付くまでにかかる回数の期待値は
３／（２2−２）＝３／２です。
よって、一旦２人になってから１人が勝ち残るまでの勝負回数の条件付き期待値は、
（１／３）×（３／２）＝１／２（回） ３→２→１の順番で決まった時の期待値はこれにＡの３／２をかけると求まります。
よって、３→２→１の回数の期待値は３／４です。
３→１、３→２→１を加えると、（３／２）＋（３／４）＝９／４となります。
一般化を意識して計算しなおすと、(3/2)*{1+(1/3)*(3/2)}です。

４人でもやってみましょう。
４人でじゃんけんをして勝負が決まるまでの回数の期待値は、
３3／（２4−２）＝27/14
勝負が決まった条件のもとで、確率とその後の期待値を表にすると次の通りです。
残り人数そうなる確率その後の期待値
２人4Ｃ2／３3＝6/272/3
３人4Ｃ3／３3＝4/274/9
よって、求める期待値は
(27/14)*{1+(6/27)*(3/2)+(4/27)*(9/4)}＝{27+6*2/3+4*9/4}/14＝45/14となります。

ｎ人への拡張

この漸化式をｎだけの式で表すことは私にとっては不可能ですが、
根性でプログラムを走らせることはできそうです。
目次へ