場合の数・確率の格言
何の問題も解かないうちからこれを覚えても意味はないと思いますが、備忘録的にまとめておきます。
「少なくとも 1 個は」とは，「さいころの 1 個以上は」1 が出ていると読解します。 直接場合分けするのは面倒だと思います。 これの余事象は，「すべて１ が出ない」となり，1 つしかなります。 これに代表されるように、「少なくとも」問題は、余事象を引いたほうが早いものがほとんどです。
条件が複数ある場合は、より条件の厳しいほうを優先させます。 基本的なことはこちらを参照してください。
一番左は、3 人選べて、中央は 2 人選べる。さらに一番右は残った 1 人だから、 3×2×1 通りです。強調した部分を最も簡単な英語で考えたら「and」ですよね。 つまり、「and」で区切られた文章を一まとめにするときは、掛け算を用います。 これを「積の法則」と呼んでいます。 詳しくはこちら
共通部分がないことを確認したら，足すだけで構いません。 共通部分があるときはもちろんその重なりを引かなくてはなりません。 代表的な問題はこちらです。
結果同じ ABC となるものは同じですから，どちらから定めてもかまいません。 例 1 で、勝手に左から決めてしまっているのは、この格言があるからです。 基本的な例題
|
確率用語辞典
|
確率を勉強するとき、独特の言い回しが壁になってしまう方もいるようです。 私はこれらを｢確率用語｣と呼んでいます。 この確率用語は避けて通れないものもあり， このサイトでも無意識に使ってしまうことが多いものを紹介します。 (このページにないものについては、必要と思われた時に説明します) |
| 試行と事象 | 何かを試しにやってみることを試行といい，試行の後に起こった｢ことがら｣を事象といいます。例えば，次のとおりです。 ｢2 つのさいころを振る」←試行 「目の和が 6 となる｣←事象 |
|---|---|
| 全事象 | 試行の結果起こり得るすべての事象。 |
| 余事象 | 事象Ａに対して、「Ａが起こらない」という事象のことです。 |
| 排反事象 互いに排反 | 複数の事象が、同時に起こらないとき、この用語を使います。 極論ですが，「事象Ａ」と「事象Ａの余事象」は、必ず互いに排反です。 |
| (互いに) 独立 | 2 つの試行が互いに影響しあわないとき，それらは互いに独立と言います。 1つめの試行でＡが起こり，かつ 2 つめの試行でＢが起こる確率について， 等式 P(Ａ∩Ｂ)＝P(Ａ)×P(Ｂ) が成り立つ状態でもあります。 |
| 根元事象 | それ以上場合分けできない事象のこと。 |
| 同様に確からしい | 複数の事象に対して、それらが起こる確率が等しいときに使います。 |
|
さいころを 2 個振って，目の和が 6 になる目の出方について， 場合の数では区別がつくかどうかで数え方が異なることがあります。 2 個のさいころに区別がつかないときは「1 + 5」「2 + 4」「3 + 3」の 3 通りなのですが… 場合の数と確率では，少しだけ事情が違うことがあります。
右図のように数字の入れ方を工夫するとすぐ出来ます。 |
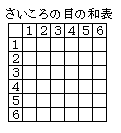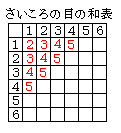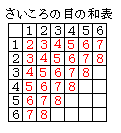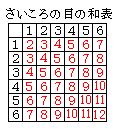｢さいころを 2 個振って，目の和が 6 となる｣確率について，